There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The test cases are generated so that the answer will be less than or equal to 2 * 109.
Example 1:
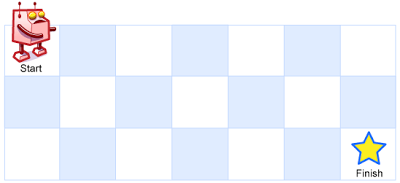
Input: m = 3, n = 7
Output: 28
Example 2:
Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
Constraints:
- 1 <= m, n <= 100
주어진 m, n 사이즈의 격자 배열 속에서 좌상단에서 우하단까지 가는 유니크한 길 갯수를 찾는 문제이다.
m-1개의 x축과 n-1개의 y축이 존재하고 m+n-2개의 순열과 같다
(m+n-2)!/(m-1)!*(n-1)! 을 계산하게 된다면 유니크한 길 갯수가 나오게 된다.
예를 들어 3, 2가 주어졌다면 5!/3!2!이므로 5*4/2*1을 계산하면 된다
이를 이용하여 코드로 작성하면 아래와 같다.
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
big, small = m-1, n-1
if m < n:
big, small = small, big
total = big + small
answer = 1
for i in range(total, big, -1):
answer *= i
for i in range(1, small+1):
answer = answer//i
return answer
문제 출처 : https://leetcode.com/problems/unique-paths/
Unique Paths - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
Github : https://github.com/kkkkang1009/leetcode/blob/master/leetcode_62.py
GitHub - kkkkang1009/leetcode: leetcode
leetcode. Contribute to kkkkang1009/leetcode development by creating an account on GitHub.
github.com
'IT > LeetCode' 카테고리의 다른 글
| [LeetCode] 64. Minimum Path Sum (0) | 2022.08.17 |
|---|---|
| [LeetCode] 63. Unique Paths II (0) | 2022.08.17 |
| [LeetCode] 58. Length of Last Word (0) | 2022.08.15 |
| [LeetCode] 53. Maximum Subarray (0) | 2022.08.15 |
| [LeetCode] 38. Count and Say (0) | 2022.07.22 |


댓글